I want to tell you about an idea that has had a huge influence on the way that I write software. And I mean that in the literal sense: it’s changed the way that I write software; it’s re-shaped my development workflow.

The idea is this: you can write programs that modify themselves.

And I don’t mean macros or metaprogramming or anything fancy like that. I mean that you can write programs that edit their own source code. Like, the files themselves. The actual text files on disk that have your source code in them.

That’s not the whole idea, though. There’s more to it: you write programs that can edit themselves, and then you use that as your REPL.

Instead of typing something into a prompt and hitting enter and seeing the output on stdout, you type something into a file and hit some editor keybinding and the result gets inserted into the file itself. Patched on disk, right next to the original expression, ready to be committed to source control.

This read-eval-patch loop is already a little useful – it’s a REPL with all of the conveniences of your favorite editor – but we’re still not done. There’s one more part to the idea.

Once you have your expression and your “REPL output” saved into the same file, you can repeat that “REPL session” in the future, and you can see if the output ever changes.

And then you use this technique to write all of your tests.

That’s the whole idea. You use your source files as persistent REPLs, and those REPL sessions become living, breathing test cases for the code you were inspecting. They let you know if anything changes about any of the expressions that you’ve run in the past. This kind of REPL can’t tell you if the new results are right or wrong, of course – just that they’re different. It’s still up to you to separate “test failures” from expected divergences, and to curate the expressions-under-observation into a useful set.

This is pretty much the only way that I have written automated tests for the last six years. Except that it isn’t really – this is the way that I haven’t written automated tests. This is the way that I have caused automated tests to appear for free around me, by doing exactly what I have always done: writing code and then running it, and seeing if it did what I wanted.

I’m exaggerating, but not as much as you might think. Of course these tests aren’t free: it takes work to come up with interesting expressions, and I have to write setup code to actually test the thing I care about, and there is judgment and curation and naming-things involved. And of course there is some effort in verifying that the code under test actually does the thing that I wanted it to do.

But the reason that it feels free is that nearly all of that is work that I would be doing already.

Like, forget about automated tests for a second – when you write some non-trivial function, don’t you usually run it a couple times to see if it actually does the thing that you wanted it to do? I do. Usually by typing in interesting expressions at a REPL, and checking the output, and only moving on once I’m convinced that it works.

And those expressions that I run to convince myself that the code works are exactly the expressions that I want to run again in the future to convince myself that the code still works after a refactor. They are exactly the expressions that I want to share with someone else to convince them that the code works. They are, in other words, exactly the test cases that I care about.

And yes, I mean, I’m still exaggerating a bit. There is a difference between expressions that you run once and expressions that you run a thousand times. In particular, you want your “persistent REPL” outputs to be relatively stable – you don’t want tests to fail because the order of keys in a hash table changed. And usually you want to document these cases in some way, to say why a particular case is interesting, so that it’s easier to diagnose a failure in the future.

But we’re getting a little into the weeds there. Let’s take a step back.

You’ve heard the idea, now let’s see how it feels. I want to demonstrate the workflow to you, but it’s going to require a little bit of suspension of disbelief on your part: this is a blog post, and I don’t really have time to show you any particularly interesting tests. I also have to confess that I don’t write very many interesting tests outside of work, so this will be a combination of completely fake contrived examples and trivial unit tests lifted from random side projects.

With that in mind, let’s start with one from the “extremely contrived” camp:

Yes, I know that you haven’t actually implemented a sorting algorithm since the third grade, but I hope that it gives you the gist of the workflow: you write expressions, press a button, and the result appears directly in your source code. It’s like working in a Jupyter notebook, except that you don’t have to work in a Jupyter notebook. You don’t have to leave the comfort of Emacs, or Vim, or VSCode, or BBEdit – as long as your editor can load files off a file system, it’s compatible with this workflow.

In case you skipped the video, the end result looks something like this:

(use judge)

(defn slow-sort [list]
  (case (length list)
    0 list
    1 list
    2 (let [[x y] list] [(min x y) (max x y)])
    (do
      (def pivot (in list (math/floor (/ (length list) 2))))
      (def bigs (filter |(> $ pivot) list))
      (def smalls (filter |(< $ pivot) list))
      (def equals (filter |(= $ pivot) list))
      [;(slow-sort smalls) ;equals ;(slow-sort bigs)])))

(test (slow-sort [3 1 2]) [1 2 3])
(test (slow-sort []) [])
(test (slow-sort [1 1 1 1 1]) [1 1 1 1 1])

Those tests at the end might look like regular equality assertions – and, in a way, they are. But I only had to write the “first half” of them – I only wrote the expressions to run in my “REPL” – and my test framework filled in right-hand sides for me.

Now, as you probably noticed, there were a lot of parentheses in that demo. Don’t be alarmed: the parentheses are entirely incidental. I just happen to be spending a lot of time with Janet lately, and I’ve written a test framework that’s heavily based around this workflow.

But there’s nothing parentheses-specific about this technique. I first met this type of programming in OCaml, via the “expect test” framework. The specifics of OCaml’s expect tests are a little bit different, but the overall workflow is the same:

let%expect_test "formatting board coordinates" =
  print_endline (to_string { row = 0; col = 0 });
  [%expect "A1"];
  print_endline (to_string { row = 10; col = 4 });
  [%expect "E11"]
;;

Instead of the expression-oriented API we saw in Janet, an OCaml expect test is a series of statements that print to stdout, followed by automatically-updating assertions about what exactly was printed. This makes sense because OCaml doesn’t really have a canonical way to print a representation of any value,¹ so you have to decide exactly what you want your REPL to Print.

And this workflow works in normal languages too! Here’s an example in Rust, using the K9 test framework:²

#[test]
fn indentation() {
    k9::snapshot!(
        tokenize(
            "
a
  b
  c
d
  e
    f
g
"
        ),
        "a ␤ → b ␤ c ␤ ← d ␤ → e ␤ → f ␤ ← ← g ␤"
    );
}

We’re pulling from the “trivial side project” category now. That’s a test I wrote for an indentation-sensitive tokenizer, but again, I just wrote an expression that I wanted to check and then checked that the result looked right. I didn’t have to spend any time crafting the token stream that I expected to see ahead of time – I only had to write down an expression that seemed interesting to me.

The fact that you don’t actually have to write the expected value might seem like a trivial detail – it’s not that hard to write your expectations down up front; people do it all the time – but it’s actually an essential part of this workflow. It’s an implausibly big deal. It is, in fact, the first beautiful thing I want to highlight about this technique:

1. When it’s this easy to write tests, you write more of them

The fact that I don’t have to type the expectation for my tests matters a lot more than it seems like it should. Like, I’m an adult, right? I can walk through that code and say “a, newline, indent, b, newline…” and I can write down the expected result. How hard can it be?

I actually just timed myself doing that: it took almost exactly 30 seconds to read this input and write out the expected output by hand (sans Unicode). 30 seconds doesn’t sound very long, but it’s friction. It was a boring 30 seconds. It’s something that I want to minimize. And what if I have 10 of these tests? That 30 seconds turns into, like, I don’t know; math has never been my strong suit. But I bet it’s a lot.

And that was an easy example! Let’s look at something more complicated: here’s one of dozens of tests for the parser that that tokenizer feeds into:

#[test]
fn test_nested_blocks()
    k9::snapshot!(
        parse(
            "
foo =
  x =
    y = 10
    z = 20
    y + z
  x
"
        ),
        "foo (n) = (let ((x (let ((y 10) (z 20)) (+ y z)))) x)"
    );
}

Of course I could have typed out the exact syntax tree that I expected to see ahead of time, but I know that I won’t do that – I don’t even want to time myself trying it. If I actually had to type the input and output for every single test, I’d just write fewer of them.

And yes, you still have to verify that the output is correct. But verification is almost always easier than constructing the output by hand, and in the rare cases where it isn’t, you still have the option to write down your expectations explicitly.

And sometimes you don’t have to verify at all! Often when I’m very confident that my code already works correctly, but I’m about to make some risky changes to it, I’ll use this technique to generate a bunch of test cases, and just trust that the output is correct. Then after I’m done refactoring or optimizing, those tests will tell me if the new code ever diverges from my reference implementation.

But I don’t just write more tests because it’s easy. I usually write more tests because it makes my job easier. Which is the next beautiful thing that I want to highlight:

2. This workflow makes tests useful immediately

We all know that tests are valuable, but they’re not particularly valuable right now. The point of automated testing isn’t to make sure that your code works, it’s to make sure that your code still works in five years, right?

But you won’t be working on this same codebase in five years. And there’s no way that you would make a change that breaks one of these subtle invariants you’ve come to rely on. The time you spend writing automated tests might help someone, eventually, but that’s time that you could instead be spending on “features” that your “company” needs to “make payroll this month.” Which means that – if you’re already confident that your code is correct – it can be tempting to not spend any time hardening it against the cold ravages of time.

But when tests actually provide immediate value to you – when writing tests becomes a useful part of your workflow, when it becomes a part of how you add new features – suddenly the equation changes. You don’t write tests for some nebulous future benefit, you write tests because it’s the easiest way to run your code. The fact that this happens to make your codebase more robust to future changes is just icing.

But in order to really benefit from this kind of testing, you might have to rethink what a “good test” looks like. Which brings me to…

3. Good tests are good observations of your program’s behavior

There are good tests, and there are bad tests. This is true whether or not you’re writing this particular style of test, but the ceiling for what a “good test” can look like is much, much higher when you’re using this technique.

I’ll try to show you what I mean. Let’s look at a test for a function that finds the winner in a game of Hex:

let%expect_test "find winning path" =
  let board = make_board ~size:5 "A4 A2 B4 B3 C3 C4 D2 D3" in
  print_s [%sexp (find_winning_path board : Winning_path.t)];
  [%expect "None"];
  play_at board "E2";
  print_s [%sexp (find_winning_path board : Winning_path.t)];
  [%expect "(Black (A4 B4 C3 D2 E2))"];

Okay. Sure. I can sort of think for a minute and see that there was no winning path until black played at E2, and then there was one, and it’s probably reporting the correct path. But let’s compare that with an alternative:

let%expect_test "find winning path" =
  let board = make_board ~size:5 "A4 A2 B4 B3 C3 C4 D2 D3" in
  print_board board (find_winning_path board);
  [%expect {|
    There is no winning path:

     1 2 3 4 5
    A . w . b .
     B . . w b .
      C . . b w .
       D . b w . .
        E . . . . .
    |}];
  play_at board "E2";
  print_board board (find_winning_path board);
  [%expect {|
    Black has a winning path:

     1 2 3 4 5
    A . w . * .
     B . . w * .
      C . . * w .
       D . * w . .
        E . * . . .
    |}];

Isn’t that better? This test has convinced me in a single glance that the code is working correctly. And if, at some point in the future, the code stops working correctly – if I refactor the find_winning_path function and break something – I claim that this test will give me a decent head start on figuring out where I went wrong.

Of course it took some work to write this visualization in the first place. Not a lot of work – it’s just a nested for loop – but still, it did take longer to write this test than the (Black (A4 B4 C3 D2 E2)) version.

This is some of my favorite kind of work, though. It’s work that will speed up all of my future development, by making it easier for me to understand how my code works – and, even better, by making it easier for other people to understand how my code works. I only have to write the print_board helper once, but I can use it in dozens of tests – and so can my collaborators.

Here’s another test that took a little work to produce, but that I found extremely useful during development:

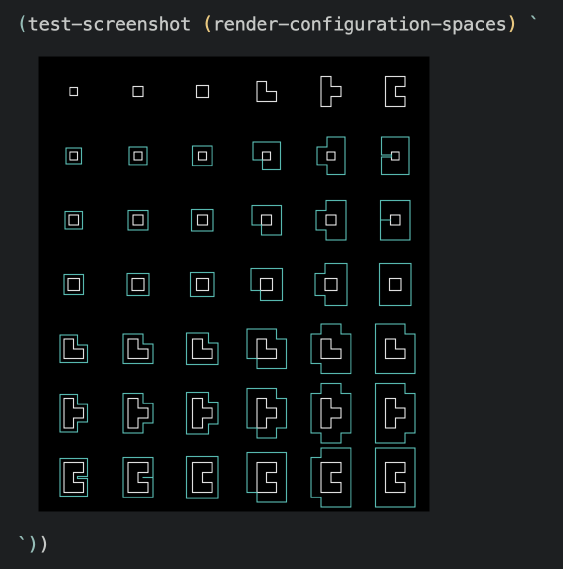
You can imagine this as taking each of the top shapes and tracing them around the perimeter of the bottom shapes, maintaining contact at all times. Sort of a tricky function to write correctly, and one where visualization really helps me see that I got it right – and, of course, to see what I did wrong when I inevitably break it.

But that’s kind of cheating: that visualization uses Emacs’s iimage-mode to render a literal image inline with my code, which is not something that you can do everywhere. And since part of the appeal of this technique is the universal accessibility, I should really stick to text.

Here, here’s a better example. This is a function that, given a source of uniformly distributed random numbers, gives you a source of normally distributed random numbers:

(defn marsaglia-sample [rng]
  (var x 0)
  (var y 0)
  (var r2 0)
  (while (or (= r2 0) (>= r2 1))
    (set x (math/rng-uniform rng))
    (set y (math/rng-uniform rng))
    (set r2 (+ (* x x) (* y y))))

  (def mag (math/sqrt (/ (* -2 (math/log r2)) r2)))
  [(* x mag) (* y mag)])

Except… does it work? I just copied this from Wikipedia; I don’t really have very good intuition for the algorithm yet. Did I implement it correctly?

It’s not immediately obvious how I would write a test for this. But if I weren’t trying to “test” it – if I just wanted to convince myself that it worked – then I’d probably plot a few thousand points from the distribution and check if they look normally distributed. And if I had any doubts after that, maybe I’d calculate the mean and standard deviation as well and check that they’re close to the values I expect.

So that’s exactly what I want my automated tests to do:

(deftest "marsaglia sample produces a normal distribution"
  (def rng (math/rng 1234))
  (test-stdout (plot-histogram |(marsaglia-sample rng) 100000) `
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣷⣾⣦⣆⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣿⣿⣿⣷⣦⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⣿⣿⣿⣿⣿⣿⣷⣦⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣆⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣧⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣤⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣶⣦⣄⡀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣶⣤⣤⣄
    μ = 0.796406
    σ = 0.601565
  `))

And hark! That’s clearly wrong. And the test tells me exactly how it’s wrong: it’s only producing positive numbers (the histogram is centered around the mean). This helps me pinpoint my mistake, and to fix it:

(defn symmetric-random [rng x]
  (- (* 2 x (math/rng-uniform rng)) x))

(defn marsaglia-sample [rng]
  (var x 0)
  (var y 0)
  (var r2 0)
  (while (or (= r2 0) (>= r2 1))
    (set x (symmetric-random rng 1))
    (set y (symmetric-random rng 1))
    (set r2 (+ (* x x) (* y y))))

  (def mag (math/sqrt (/ (* -2 (math/log r2)) r2)))
  [(* x mag) (* y mag)])

(deftest "marsaglia sample produces a normal distribution"
  (def rng (math/rng 1234))
  (test-stdout (plot-histogram |(marsaglia-sample rng) 100000) `
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⣦⣾⣿⣦⣀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣴⣿⣿⣿⣿⣿⣿⣆⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣠⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣴⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣦⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⣠⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⡀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⢀⣴⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣶⡀⠀⠀⠀⠀⠀⠀
    ⢀⣀⣀⣤⣶⣾⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣶⣤⣀⣀⡀
    μ = 0.001965
    σ = 0.998886
  `))

And, like, yes: writing this test required me to write a Unicode histogram plotter thingy, like a crazy person. But I’ve already written a Unicode histogram plotter thingy, like a crazy person, so I was able to re-use it here – just as I will be able to re-use it again in the future, the next time I feel like it will be useful.

In fact I’ve accumulated a lot of little visualization helpers like this over the years – helpers that allow me to better observe the behavior of my code. These helpers are useful when I’m writing automated tests, because they help me understand when the behavior of my code changes, but they’re also useful for regular ad-hoc development. It’s useful to be able to whip up a histogram, or a nicely formatted table,³ or a graph of a function, when I’m doing regular old printf debugging.

Which reminds me…

4. You can use printf debugging right in your tests

I’ve shown you two types of these “REPL tests” so far.

There’s a simple expression-oriented API:

(test (+ 1 2) 3)

And there’s the imperative stdout-based API:

let%expect_test "board visualization" =
  print_board (make_board ~size:5 "A4 A2 B4 B3 C3 C4 D2 D3");
  [%expect {|
     1 2 3 4 5
    A . w . b .
     B . . w b .
      C . . b w .
       D . b w . .
        E . . . . .
    |}];

When I first starting writing tests like this, the stdout-based API seemed a little weird to me. Most of my tests just printed simple little expressions, and the fact that I had to spread that out across multiple lines was annoying. And if I did want to create a more interesting visualization, like the one above, couldn’t I just write an expression to return a formatted string?

Yes, but: print is quick, easy, and familiar. It’s nice that rendering that board was just a nested for loop where I printed out one character at a time. Of course I could have allocated some kind of string builder, and appended characters to that, but that’s a little bit more friction than just calling print. I’d rather let the test framework do it for me automatically: the easier it is to write visualizations like this, the more likely I am to do it.

But when I actually spent time writing tests using this API, I came to really appreciate a subtle point that I had initially overlooked: stdout is dynamically scoped.

Which means that if I call print in a helper of a helper of a helper, it’s going to appear in the output of my test. I don’t have to thread a string builder through the call stack; I can just printf, and get printf-debugging right in my tests.

For example: our function to make normally distributed random numbers relies on “rejection sampling” – we have to generate uniformly distributed random numbers until we find a pair that lies inside the unit circle.

I’m curious how often we actually have to re-roll the dice. It’s not an observable property of our function, but we can just print it out in the implementation:

(defn marsaglia-sample [rng]
  (var x 0)
  (var y 0)
  (var r2 0)
  (var iterations 0)
  (while (or (= r2 0) (>= r2 1))
    (set x (symmetric-random rng 1))
    (set y (symmetric-random rng 1))
    (set r2 (+ (* x x) (* y y)))
    (++ iterations))
  (def rejections (- iterations 1))
  (when (> rejections 0)
    (printf "rejected %d values" rejections))

  (def mag (math/sqrt (/ (* -2 (math/log r2)) r2)))
  [(* x mag) (* y mag)])

And then re-run our test, exactly like we did before:

(deftest "marsaglia sample produces a normal distribution"
  (def rng (math/rng 1234))
  (test-stdout (plot-histogram |(marsaglia-sample rng) 100) `
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    rejected 2 values
    rejected 1 values
    rejected 1 values
    rejected 1 values
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇⠀⠀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇⠀⡀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇⠀⡇⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡄⢠⠀⢸⣤⡄⡇⢠⣧⡇⡄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢠⢠⡇⢸⡄⣼⣿⡇⡇⢸⣿⡇⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡆⡆⠀⢸⢸⡇⢸⡇⣿⣿⡇⡇⣾⣿⡇⡇⠀⠀⠀⢰⡆⠀⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⠀⠀⠀⡆⠀⠀⠀⡇⣷⣶⢸⣾⣷⣾⣷⣿⣿⣷⣷⣿⣿⣷⡇⢰⡆⠀⣾⡇⡆⠀⠀⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⢰⠀⠀⡇⠀⡆⡆⣷⣿⣿⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢸⣷⡆⣿⡇⣷⢰⡆⠀⠀⠀⠀⠀⠀
    ⠀⠀⠀⢸⢸⡇⡇⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⣿⣿⣿⣿⡇⣿⠀⠀⠀⠀⠀
    μ = -0.054361
    σ = 1.088199
  `))

Alright, so we rejected 33 points, which means that we generated 133 – a rejection rate of around 25%. The area of the unit circle is π, and the area of its bounding square is 4, so I’d expect us to reject around (1 - π/4) ≈ 21.5% of points. Pretty close!

Now, this is the sort of thing that I wouldn’t keep around in an automated test. This was exploratory; this was a gut check. That output is not in a very useful format, and I don’t think it’s really worth ensuring that this rate remains stable over time – I can’t imagine that I’ll screw that up without breaking the function entirely. But the important takeaway is that it was really, really easy to sprinkle printfs into code, and to see their output right next to the code itself, using the exact same workflow that I’m already using to test my code.

And while this output was temporary, I actually do wind up committing many of the exploratory expressions that I run as I’m developing. Because…

5. Good tests make good documentation

Compare:

sep-when is a function that takes a list and a predicate, and breaks the input list into a list of sub-lists every time the predicate returns true for an element.

With:

(test (sep-when [1 2 3 5 3 6 7 8 10] even?)
  [[1] [2 3 5 3] [6 7] [8] [10]])

My brain can intuitively understand the behavior of this function from the example code more easily than it can parse and understand the (ambiguous!) English description. The description is still helpful, sure, but the example conveys more information more quickly. To me, anyway.

I think that this is mostly because my brain is very comfortable reading REPL sessions, which might not be true for everyone. And I’m not saying that good English-language documentation isn’t important – ideally, of course, you have both. But there are two important advantages to the second version:

1. Tests don’t lie; they can’t become stale.

2. I didn’t have to write it.

I spent a couple minutes trying to come up with a pithy English description of this function, and I don’t even think I did a very good job. Writing good documentation is hard, but generating examples is easy – especially when my test framework is doing half the work.

And since it’s easy to generate examples, I do it in cases where I wouldn’t have bothered to write documentation in the first place. This sep-when example was a real actual helper function that I pulled from a random side project. A private, trivial helper, not part of any public API, that I just happened to write as a standalone function – in other words, not the sort of function that I would ever think to document.

It’s also a trivial function, far from the actual domain of the problem I was working on, so it’s not the sort of thing I would usually bother to test either. And I might regret that – bugs in “trivial” helpers can turn into bugs in actual domain logic that can be difficult to track down, and I probably only have a 50/50 shot of getting a trivial function right on the first try in a dynamically-typed language.

But when the ergonomics of writing tests is this nice, I actually do bother to test trivial helpers like this. Testing just means writing down an expression to try in my “REPL,” and I can do that right next to the implementation of the function itself:

(defn sep-when [list f]
  (var current-chunk nil)
  (def chunks @[])
  (eachp [i el] list
    (when (or (= i 0) (f el))
      (set current-chunk @[])
      (array/push chunks current-chunk))
    (array/push current-chunk el))
  chunks)

(test (sep-when [1 2 3 5 3 6 7 8 10] even?)
  [[1] [2 3 5 3] [6 7] [8] [10]])

Which means that, not only will I catch dumb mistakes early, but I also automatically generate examples for myself as I code. If I come back to this code a year from now and can’t remember what this function was supposed to do, I only have to glance at the test to remind myself.

And on, and on…

I could keep going, but I think that my returns are starting to diminish here. If you still aren’t convinced, James Somers wrote an excellent article about this workflow that I would recommend if you want to see more examples of what good tests can look like in a production setting.

But I think that it’s difficult to convey just how good this workflow actually is in any piece of writing. I think that it’s something you have to try for yourself.

And you probably can! This technique is usually called “inline snapshot testing,” or sometimes “golden master testing,” and if you google those phrases you will probably find a library that lets you try it out in your language of choice. I have personally only used this technique in OCaml, Janet, and Rust, but in the spirit of inclusivity, I also managed to get this working working in JavaScript, in VSCode, using a test framework called Jest:

I will be the first to admit that that workflow is not ideal; Jest is absolutely not designed for this “read-eval-patch-loop” style of development. Inline snapshots are a bolted-on extra feature on top of a traditional “fluent” assertion-based testing API, and it might take some work to twist Jest into something useful if you actually wanted to adopt this workflow in JavaScript. But it’s possible! The hard part is done at least; the source rewriter is written. The rest is just ergonomics.

There is a cheat code, though, if you cannot find a test framework that works in your language: Cram.

Cram is basically “inline snapshot tests for bash,” but since you can write a bash command to run a program written in any other language, you can use Cram as a language-agnostic snapshot testing tool. It isn’t as nice as a native testing framework, but it’s still far, far nicer than writing assertion-based tests. And it works anywhere – I use Cram to test the test framework that I wrote in Janet, for example, since I can’t exactly use it to test itself.

Okay. I really am almost done, but I feel that I should say one last thing about this type of testing, in case you are still hesitant: this is a mechanic. This is not a philosophy or a dogma. This is just an ergonomic way to write tests – any tests.

You can still argue as much as you want about unit tests vs. integration tests and mocks vs. stubs. You can test for narrow, individually significant properties, or just broadly observe entire data structures. You can still debate the merits of code coverage, and you can even combine this technique with quickcheck-style automatic property tests. Here, look:

module Vec2 = struct
  type t =
    { x : float
    ; y : float
    } 
  [@@deriving quickcheck, sexp_of]

  let length { x; y } =
    sqrt (x *. x +. y *. y)
  ;;

  let normalize point =
    let length = length point in
    { x = point.x /. length
    ; y = point.y /. length 
    }
  ;;
end

Pretty simple code, but does it work for all inputs? Well, let’s try a property test:

let assert_nearly_equal here actual expected ~epsilon =
  [%test_pred: float]
    ~here:[here]
    (fun actual -> Float.( < ) (Float.abs (actual -. expected)) epsilon)
    actual

let%expect_test "normalize returns a vector of length 1" =
  Quickcheck.test [%quickcheck.generator: Vec2.t]
    ~sexp_of:[%sexp_of: Vec2.t]
    ~f:(fun point ->
      assert_nearly_equal [%here] (Vec2.length (Vec2.normalize point)) 1.0 ~epsilon:0.0001)
[@@expect.uncaught_exn {|
  (* CR expect_test_collector: This test expectation appears to contain a backtrace.
     This is strongly discouraged as backtraces are fragile.
     Please change this test to not include a backtrace. *)

  ("Base_quickcheck.Test.run: test failed"
    (input ((x -3.3810849992682576E+272) (y 440.10383674821787)))
    (error
      ((runtime-lib/runtime.ml.E "predicate failed"
         ((Value 0) (Loc test/demo.ml:20:15) (Stack (test/demo.ml:29:26))))
         "Raised at Ppx_assert_lib__Runtime.test_pred in file \"runtime-lib/runtime.ml\", line 58, characters 4-58\
        \nCalled from Base__Or_error.try_with in file \"src/or_error.ml\", line 84, characters 9-15\
        \n")))
  Raised at Base__Error.raise in file "src/error.ml" (inlined), line 9, characters 14-30
  Called from Base__Or_error.ok_exn in file "src/or_error.ml", line 92, characters 17-32
  Called from Expect_test_collector.Make.Instance_io.exec in file "collector/expect_test_collector.ml", line 262, characters 12-19 |}]
;;

This is not, you know, a good property test, but just focus on the workflow – even though it’s just an assertion failure, it’s nice to see that error in context. I don’t need to manually correlate line numbers with my source files, even if I’m working in a text editor that can’t jump to errors automatically.

So the mechanic of source patching is still somewhat useful regardless of what sort of tests you’re writing. This post has focused on pretty simple unit tests because, you know, it’s a blog post, and we just don’t have time to page in anything complicated together. And I’ve especially emphasized testing-as-observation because that happens to be my favorite way to write most tests, and it’s a unique superpower that you can’t really replicate in a traditional test framework.

But that doesn’t mean that read-eval-patch loops are only useful in these cases, or that you can only adopt this technique with a radical change to the way you think about testing.

Although it might not hurt…