In the very first post of this series, I talked about how I wrote a simple raycaster for calculating field of view in my little 2D game.

Nothing fancy; this was, as you may recall, a Sunday afternoon project.

The output of my raycaster was just a collection of points where each ray terminated.

These points represent the terminals of rays cast towards every vertex in this simple scene:

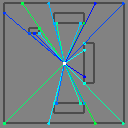
In order to draw the area “covered by” the points – the actual field of view – we need to fill in the spaces between them with triangles:

Which is exactly what you saw in the FOV video above. The triangles are hiding a little, but we can outline them to make it more clear where the area comes from:

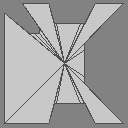
Neat. The final FOV looks like kind of a complex polygon, but it’s actually just a fan of irregular triangles that all share the same centerpoint.

But in order to draw that triangle fan, it’s important that all the points be sorted in the right order. Because if we draw them out of order…

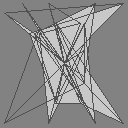
We get garbage, basically.

But kinda weird garbage! Why are some of the triangles empty?

You might expect to see something like this:

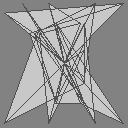
But even though we’re only rendering 2D images, we’re still using OpenGL. And in OpenGL, triangles are actually three-dimensional. And only triangles whose points are defined in a clockwise order¹ face towards the camera; the rest face away from us, and by default Raylib won’t draw the “backs” of triangles.²

But that’s sort of just a fun tangent. We don’t want either of those incorrect triangulations; we want to draw this triangle fan:

And in order to do that, we need to sort the points. We need to turn this collection of scattered rays:

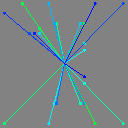
Into this neatly sorted list:

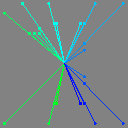
this is too many pictures

Okay, yes. I might be drunk on writing tests with pictures in them. The power might be going to my head.

So let’s switch to words now: we have some points; we need to sort the points. Easy, right?

A point is just an [x y] pair, and we can take the arctangent – (math/atan2 y x) – to find the angle that it makes with the x-axis. Then we can sort by that angle, and then… we’re done. That’s all there is to it.

But, of course, we’re not going to do that.

That would be boring. That wouldn’t be a blog post. We’re going to do something weird and fiddly and complicated instead.

Because you can’t use trigonometry in a game. Trigonometric functions are slow! Think of how many cycles an atan call takes. No, I don’t know either. But probably a lot. Then multiply that by the number of ray terminals, and then think about doing that on every frame?? My gosh. The lavishness. The extravagance. We could never get away with that in today’s computational climate.

And yes, I do realize that I’m writing a game in a garbage-collected, dynamically-typed, interpreted language right now. Any discussion about performance in this context is a little… quaint. And, like, maybe if I were to rewrite the raycaster component in C, then the trigonometric functions would be a bottleneck here… but we’d still want to profile and there’s a good chance that this would never ever matter.

But whatever. Let’s live a little. Let’s prematurely optimize this thing.

So I looked around, it didn’t take long before I found this StackOverflow answer, which claims to sort points in a circle without any trigonometry in sight:

bool less(point a, point b)
{
    if (a.x - center.x >= 0 && b.x - center.x < 0)
        return true;
    if (a.x - center.x < 0 && b.x - center.x >= 0)
        return false;
    if (a.x - center.x == 0 && b.x - center.x == 0) {
        if (a.y - center.y >= 0 || b.y - center.y >= 0)
            return a.y > b.y;
        return b.y > a.y;
    }

    // compute the cross product of vectors (center -> a) x (center -> b)
    int det = (a.x - center.x) * (b.y - center.y) - (b.x - center.x) * (a.y - center.y);
    if (det < 0)
        return true;
    if (det > 0)
        return false;

    // points a and b are on the same line from the center
    // check which point is closer to the center
    int d1 = (a.x - center.x) * (a.x - center.x) + (a.y - center.y) * (a.y - center.y);
    int d2 = (b.x - center.x) * (b.x - center.x) + (b.y - center.y) * (b.y - center.y);
    return d1 > d2;
}

Neat! But also… whoa. That’s a lot of code compared to atan.

And looking through it, it’s not really clear what’s… happening.

What are those weird checks at the beginning? Why is there a special case when x == 0? That seems gross; I don’t wanna do that. And then it’s using the distance from the center to tie-break in two different places?? No; that’s nonsense; get out of here.

But the gist seems to be sorting by… the cross product of the vectors?

I don’t know why that would work, but let’s try it and find out. I’m sure all the rest of that stuff isn’t that important.

(defn clockwise-comparator [a b]
  (let [det (cross a b)]
    (cond
      (< det 0) true
      (> det 0) false
      (let [distance-a (mag-squared a)
            distance-b (mag-squared b)]
        (> distance-a distance-b)))))

(sort ray-hits clockwise-comparator)

Well, that seems to work just fine, past Ian thought, and he continued on his merry way.

Which brings us back to this bug:

Because it turns out sorting by the cross product like this almost works. It will usually put points in the right order, but occasionally it won’t. And presumably those special cases are there to resolve… whatever problem it is that we’re seeing. I don’t know. I don’t understand any of this code.

So let’s try to fix that.

// compute the cross product of vectors (center -> a) x (center -> b)
int det = (a.x - center.x) * (b.y - center.y) - (b.x - center.x) * (a.y - center.y);

First things first: that comment says that it’s taking the cross product of the two vectors. But we remember from high school physics that the cross product of two vectors is a third vector that is perpendicular to the two input vectors. And we also remember that it’s only defined in three dimensions, because linear algebra is dumb and weird. Also something about right-handedness. Whatever.

But this random StackOverflow answer I found defines the “cross product” as (paraphrasing here):

a.x * b.y - b.x * a.y

Which is a scalar, not a vector. And it calls this value “det,” which makes me think of “determinant,” although that’s another word that I only half-remember from my book-learnin' days.

This is not actually mysterious, though, once we spend a minute thinking about it.

Our vectors are two-dimensional, but we can imagine them as three-dimensional vectors with z = 0. This means that the (three-dimensional) cross product is only going to have a z value – x and y will always be 0. The only vectors perpendicular to the plane of our screen are vectors sticking straight out of the screen towards us or vectors sticking straight into our screen away from us.

So we’re actually calculating the z component of the three-dimensional cross-product. And since the z component is the only component of that vector, we can get away with calling it the cross product.

The z component of the cross product also happens to be the determinant of this two-dimensional matrix:

⎡ a.x  b.x ⎤
⎣ a.y  b.y ⎦

Which explains the det identifier, I guess. But this is no help: determinants have never made any sense to me. I remember that the determinant is, like, the area of a parallelogram or something, but I don’t really have any parallelograms on me right now so let’s try something else.

Okay, so do you remember the right-hand rule? I sort of vaguely recall that you use it to determine the sign of the cross product. You curl your fingers from one vector to the other, and then you look at where your thumb is pointing, and that tells you… like, the direction of the resulting vector? But here we’re actually going to do the reverse thing: we know whether z is positive or negative – we know which way to point our thumb. And that tells us which way to curl our fingers – and then we can look at our fingers and see if they’re curling clockwise or counterclockwise.

Okay, so that’s some intuition for this answer, at least. That sort of tells us why we’re looking at the sign of the cross product.

But what is that value? Geometrically, I mean. I get that we’re multiplying xs and ys and subtracting and getting a number but, like, what is that number? What does it mean?

Well it turns out that number is the product of the magnitude of the two vectors and the sine of the angle between them.

wait what

Wait what indeed. This seems sort of magical, right?

(cross a b) = (* (mag a) (mag b) (math/sin theta))

Where theta is the angle between a and b.

But we don’t know the angle between a and b!

And, I mean, we still don’t – we don’t get to learn the angle by doing this; we only get to learn the sine of the angle – which is just the ratio of the lengths of the edges of a right triangle. So there’s no actual magic happening here.

Still, it was not at all obvious to me why this cross product was related to the sine in this way. Why are we multiplying xs with ys? Why is there a subtraction? What’s going on here?

So I sat down with a piece of paper and tried to derive it. It was actually a lot simpler than I was expecting: take the two vectors and pretend that they form the hypotenuses of two right triangles. You know how to calculate the sine of the angles they make with the x-axis, and the angle between them is just the difference between their angles to the x-axis.

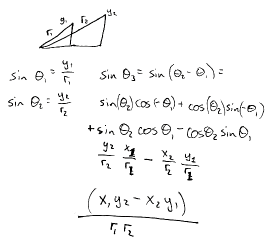
The key bit is this little trigonometric identity:

sin(θ₁ + θ₂) = sin(θ₁)cos(θ₂) + cos(θ₁)sin(θ₂)

Which I did not derive myself. I just half-remembered that it should be a thing and looked up a table of trigonometric identities.

That identity is the only reason we end up multiplying xs and ys – because sines become ys and cosines become xs. The reason that the product of the magnitudes of the vectors shows up in the final cross product is that those are the lengths of the hypotenuses, and we don’t bother to divide them out.

That derivation also uses these other, simpler identities:

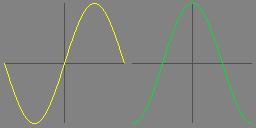
sin(-θ) = -sin(θ)
cos(-θ) = cos(θ)

Which we don’t actually need to look up – they’re apparent from the visual symmetry of the graph of the sine and cosine functions:

Trigonometry, heck yeah. Let’s keep this good thing going.

What if we do the same thing with cosine? It has a slightly different identity:

cos(θ₁ + θ₂) = cos(θ₁)cos(θ₂) - sin(θ₁)sin(θ₂)

But we can do the exact same series of substitutions:

cos(θ₂ - θ₁) = cos(θ₂)cos(-θ₁) - sin(θ₂)sin(-θ₁)
cos(θ₂ - θ₁) = cos(θ₂)cos(θ₁) + sin(θ₂)sin(θ₁)
cos(θ₂ - θ₁) = (x₂/r₂)(x₁/r₁) + (y₂/r₂)(y₁/r₁)
cos(θ₂ - θ₁) = (x₁x₂ + y₁y₂) / (r₁r₂)

Which is a decent derivation for that other extremely common vector operation, the dot product:

a · b = a.x * b.x + a.y * b.y = ǁaǁ * ǁbǁ * cos(θ)

So: when you see cross product, think sine. When you see dot product, think cosine.

Which is not, perhaps, very useful intuition. We’ll talk about a more useful intuitive interpretation of dot and cross products in a later post, but for now, just to review:

a · b = a.x * b.x + a.y * b.y = ǁaǁ * ǁbǁ * cos(θ)
a × b = a.x * b.y - a.y * b.x = ǁaǁ * ǁbǁ * sin(θ)

Being sloppy and using a × b to mean “the z component of the cross product of these two two-dimensional vectors in three dimensions.”

can we get back to programming

Yes! Let’s return to our comparator:

(defn clockwise-comparator [a b]
  (let [det (cross a b)]
    (cond
      (< det 0) true
      (> det 0) false
      (let [distance-a (mag-squared a)
            distance-b (mag-squared b)]
        (> distance-a distance-b)))))

So what we’re really comparing here is the sign of the sine between these two vectors. If the sine is positive, we say that a is clockwise from b. If the sine is negative, we say that a is counterclockwise from b. (If the sine is zero, the two points are co-linear with the origin, so we choose whichever point is farther away.)

So, does this comparator make sense?

No! It doesn’t. This relation is not transitive. So when we sort by it, we’re going to get weird results depending on the order that Janet’s sort happens to compare elements.

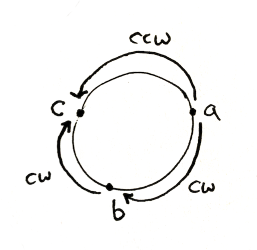
a < b, b < c, but c < a. That’s not gonna work out for us. Also: what happens when the sine is zero? We’re going to get inconsistent results when two points are co-linear with the origin, but lie on opposite sides of it.

So now we can understand that little preamble in the StackOverflow answer we’re shamelessly copying from:

if (a.x - center.x >= 0 && b.x - center.x < 0)
    return true;
if (a.x - center.x < 0 && b.x - center.x >= 0)
    return false;
if (a.x - center.x == 0 && b.x - center.x == 0) {
    if (a.y - center.y >= 0 || b.y - center.y >= 0)
        return a.y > b.y;
    return b.y > a.y;
}

That resolves the transitivity problem by saying that if the two vectors are on different sides of the y-axis, the one to the right is always clockwise from the one on the left. Or maybe the opposite of that. I dunno. It doesn’t matter.

Basically, it separates the sort into two stages: first it assigns the points an absolute ordering – left or right half – and then it break ties within each half by sorting the points relative to one another, by looking at the sine between them.

But this does not resolve the co-linearity problem. It does not solve the problem where the sine is zero but the points lie on opposite sides of the x-axis. So there’s another special case up there for that: sort points differently if they lie directly on the y-axis, which is the only point where this ambiguity is possible.

So that’s gross. But the idea is good, I think – we just need to take it one step further.

Instead of sorting the points into two halves, we can sort them into four quadrants. That feels simpler to me, because then we don’t have to worry about ever comparing points that lie 180° apart, and it’s very easy to convince ourselves that the sine-sign comparison is transitive when we’re only looking at points that lie in the same quadrant.

And by using quadrants instead of halves, we can express this comparator as a composition of smaller comparators, since we don’t need to have the distance tie-breaker happen in two different places. This might be less efficient than one big function that does all the comparisons, but it’ll be a whole lot nicer to read.

So let’s try that!

Janet’s standard library is quite minimal, so in order to write this the way I want to, we have to define some helpers for composing comparators.

First off, let me pass a list of comparators, and try them in order until one of them says there’s no equality:

(defn- comparing-helper [a b comparators]
  (if (empty? comparators)
    false
    (case ((first comparators) a b)
      -1 true
      0 (comparing-helper a b (drop 1 comparators))
      1 false)))

(defn comparing [& comparators]
  (fn [a b] (comparing-helper a b comparators)))

So, annoyingly, although Janet does support destructuring assignments, it doesn’t support head/tail destructuring or complex pattern matching on tuples. You can’t write:

(def [head ;tail] [1 2 3 4 5])

Or:

(def [head & tail] [1 2 3 4 5])

Or anything like that that you might expect coming from lisp or OCaml or Haskell or another language where the linked list is a very common first-class data type. It does support this in function parameter lists, but not normal assignments or match statements.

This feels like a weird missing feature, but okay sure whatever.

Because remember that these aren’t lists in the first place. These are immutable arrays that we’re actually slicing into. We aren’t recursing nicely on the tail of the list, but actually allocating a new array at every step of the iteration. Which is… very ineffecient.

I want Janet to have lists, and I want to write a function like this:

(defn- comparing-helper [a b comparators]
  (match comparators
    [] false
    [compare & fallbacks]
      (case (compare a b)
        -1 true
        0 (comparing-helper a b fallbacks)
        1 false)))

Because my brain is so used to this kind of recursion. But that is not the Janet way, apparently. I should just be writing an imperative loop with an early return, but… that just reads so poorly to me. So I’m sticking with my worst-of-both-worlds solution above.

Anyway.

The next helper we need is much simpler. This is a bit like Haskell’s on, or OCaml’s Comparable.lift:

(defn by [f &opt comparator]
  (default comparator cmp)
  (fn [a b] (comparator (f a) (f b))))

Easy stuff, but it’s a nice example of how default arguments look in Janet. No complaints there.

Lastly, we need to define some helpers specific to this one problem:

(defn quadrant [[x y]]
  (case [(neg? x) (neg? y)]
    [false false] 3
    [true false] 2
    [true true] 1
    [false true] 0))

(defn sign [x] (cond (< x 0) -1 (> x 0) 1 0))

(defn sine-sign [a b] (sign (cross a b)))

And then we can finally sort our points:

(sort points (comparing (by quadrant) sine-sign (by mag-squared)))

Neat! This reads better to me than the original StackOverflow answer did, although I realize that is a personal preference. It’s probably a lot less efficient with all those functions flying around, but ehhhh that’s something an optimizing compiler would be able to take care of. If it existed.

In any case, tests pass:

I mean, that one test passes. Like I said before, if we really cared about the correctness of this function over time, we would probably want to write a property test that compared it against the trivial atan implementation.

But we don’t. This function was just an excuse to talk about the relationship between trigonometry and vector operations.

And I think, by this point, we’ve done plenty of that.