One of my favorite SDF techniques is domain repetition:
I made something that I think is pretty neat, and I want to tell you about it.

This is a little hot air balloon made out of alternating layers of brass and bronze that stack together with these angled facets:
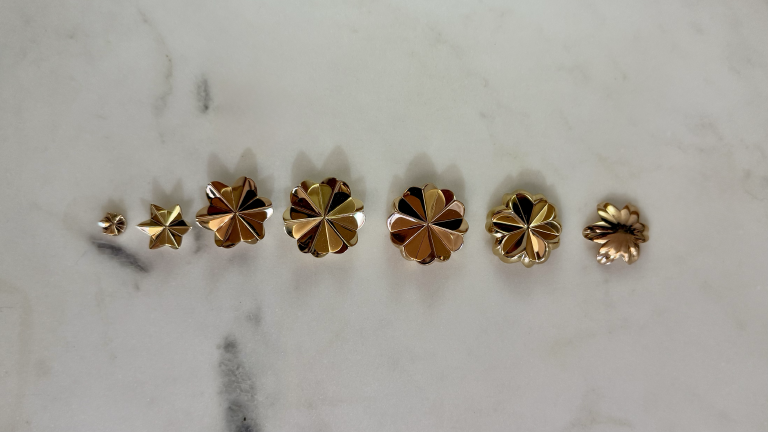
It’s 3D printed, sort of, but it really is solid metal – it’s not a metallic filament. It’s made by “lost wax casting,” where you 3D print a model out of resin, then pack it in plaster, and then once the plaster dries you melt out the resin and fill the void with molten–
You know what? This is neat, but this actually isn’t what I wanted to tell you about.
Take a look at this:
This is a triangulation of a set of random points, such that all the points are connected to one another, all of the faces are triangles, and the edges include the convex hull of the points.
I would like to claim that this is not a very “good” triangulation. This algorithm tends to produce lots of long, slivery triangles, and a really uneven distribution of edge counts across different vertices – some vertices have way more edges than they need to.
Here’s a different triangulation. These are the exact same points, but I triangulated them smarter:
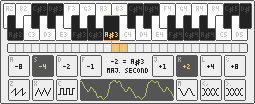
I had an idea that I wanted to try, so I tried it. You can try it too, by clicking below. Unless you’re on your phone. You can’t really try it on your phone. It needs a physical keyboard.
Hold the keys on the home row to change the pitch, and hold spacebar to play the currently selected note. You can also change the oscillator waveform, but it’s not going to win any awards for its sound synthesis.
It’s not going to win any awards as anything, really. It’s not a very good instrument!
So let’s talk about the problems, and see if we can do anything to improve them.

I’ve always been attracted to chording keyboards in theory, but I lack whatever childhood musical training is required to wrap my fingers around them.
So I made something else: an arpeggio keyboard.
Peggi is an eight-key keyboard that fits on the back of your phone. While chording keyboards require you to press multiple keys at the same time, arpeggio keyboards only ask that you type multiple keys in sequence.
Look, you already know that tmux lets you split your terminals or whatever. You know it lets you maintain remote sessions like a supercharged nohup. Neither of these features are very interesting, if you’re using a modern terminal emulator (or a tiling window manager) and doing your development locally.
So you’ve never tried tmux. People raved about it, but you didn’t listen: you’re not in the target audience. tmux is not for you.
I am projecting, obviously: that was my impression of tmux, a few years ago. Before I tried it. Before I learned how wrong I was.
Given the contents of my bar:
$ cat facts/bar
brandy
dry vermouth
lemon
light rum
lime
orange liqueur
reposado tequila
sugar
And my cocktail recipe book:
$ head facts/recipes
martini <- london dry gin
martini <- dry vermouth
daiquiri <- light rum
daiquiri <- lime juice
daiquiri <- simple syrup
margarita <- blanco tequila or reposado tequila
margarita <- lime juice
margarita <- orange liqueur
margarita <- lime wedge
...
What cocktails can I mix?
$ cat results/mixable
daiquiri
margarita
sidecar
Gosh, that’s not very many. What could I add to my bar to expand my options?
$ cat results/shopping-list
london dry gin -> gimlet
london dry gin -> martini
champagne -> airmail
cognac -> between-the-sheets
sherry -> sherry-cobbler
rhum agricole -> ti-punch
We all know the absolute minimum every software developer must know about Unicode. We aren’t bad citizens of the internet, spreading malice and encoding errors willy-nilly around the world. We’re good people, just trying to get by.
But knowing the minimum is starting to bother us. And the more we think about UTF-8 and text encoding, the more we realize that we don’t “get it” at a messy, squishy level. We’ve read about it, sure, but we’ve never actually wrapped our hands around it and felt the blood pump through its veins.
So that’s what we’re going to do in this post: grab UTF-8 by the bytes and squeeze some real understanding out of it.
Let’s do something extremely simple:

We’ve got a view controller, it has a user, the user’s got a username, and we want to show that in our navbar title. With an @ in front, because that’s what all the cool kids do these days. Simple, right?
- (void)viewDidLoad {
[super viewDidLoad];
self.title = [NSString stringWithFormat:@"@%@", self.user.username];
}
Yep! That’s all it takes. As long as the username never changes.